こんにちは。志學舎南大沢教室の館野です。

 

今回は直角三角形の三辺の長さの組み合わせについて考えます。

 

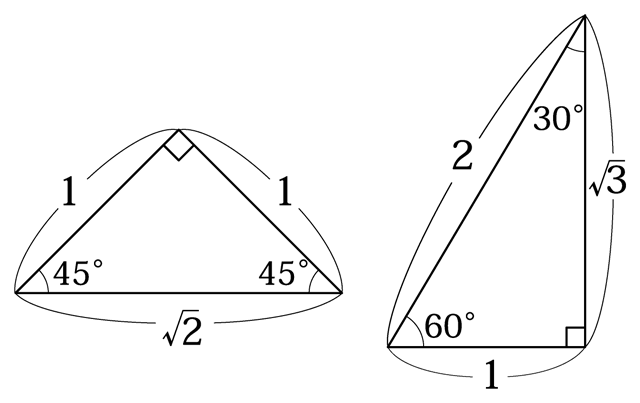
よく出てくる直角三角形の三辺の長さの比、例えば、直角二等辺三角形1：1：√2や、内角が30・60・90度の直角三角形1：2：√3、他に3：4：5など、よく出てくるものは覚えて使っていることも多いと思われます。
では、直角三角形の三辺の長さが「整数になるような組み合わせ」を見つけるにはどうしたらよいでしょうか？

以下の方法は、中学校の学習範囲の「展開と因数分解」と「三平方の定理」を組み合わせて考えると導き出せるものです。もちろん、全ての整数比を表すものではありませんが、このパターンで相似ではない三辺の組み合わせを無限に作ることができます。

 

《　ある奇数　：　（ある奇数×ある奇数－1）÷2　：　ある奇数×ある奇数+1÷2　》
ある奇数＝３なら　３：４：５
ある奇数＝５なら　５：１２：１３
ある奇数＝７なら　７：２４：２５　…

 

みなさんも自分なりの組み合わせを導き出す技を考えてみてください。よいものを閃いたらぜひ教えてくださいね。

 

 

[公式]志學舎東進ＨＰ　校舎長メッセージを更新しました！

 

 

 

---