中学受験
Let’s算数 ―整数分野の問題―
こんにちは!志學舎立川教室の安村です。今回は整数分野のわり切れる回数の解き方を紹介します。
問題 ~わり切れる回数~
24を素因数分解すると
24=2×2×2×3
となり、2が3個あるので、24は2で3回わり切れます。この考え方を利用して、次の問題を解いてみましょう。
A=1×2×3×4×・・・・・・× 29 × 30
(1)Aを2でわり続けるとき、何回目ではじめて商が整数でなくなりますか。
(2)Aは一の位から0が何個連続してならびますか。
解き方
(1) Aを素因数分解したとき、2が全部で何個あるかを調べればよいことになります。
そこで、下の図のように、30までの整数について、素因数分解したときの2の個数だけ○をつけてみましょう。
各段の○の個数を計算で求めると次のようになります。
1段目の○:2の倍数につく →30÷2=15 →15個
2段目の○:2×2(=4)の倍数につく →30÷4=7あまり2 →7個
3段目の○:2×2×2(=8)の倍数につく →30÷8=3あまり6 →3個
4段目の○:2×2×2×2(=16)の倍数につく →30÷16=1あまり14 →1個
5段目の○:2×2×2×2×2(=32)の倍数につく →なし

したがって、2の個数は全部で、
15+7+3+1=26(個)
ですから、2で26回わり切れ、(26+1=)27回目ではじめて商が整数でなくなります。
(2) Aが10で何回わり切れるかを求めればよいことになります。
10=2×5
より、Aを素因数分解したとき、[2,5]が1組あるごとに10で1回わり切れます。
(1)と同じように、30までの整数について、素因数分解したときの5の個数だけ○をつけていくと、下のようになり、
1段目の○:5の倍数につく →30÷5=6 →6個
2段目の○:5×5(=25)の倍数につく →30÷25=1あまり5 →1個
3段目の○:5×5×5(=125)の倍数につく →なし
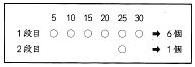
したがって、5の個数は全部で、
6+1=7(個)
(1)より2の数は26個で、5の個数は2の個数より少ないので、[2,5]の組は7組できることになります。したがって、Aは一の位から0が7個連続してならびます。
以上で今回のLet’s算数を終わります。また次回!(出典:予習シリーズ算数5年下)
東進衛星予備校 立川駅南口校 教室長 石田 康治
〒190-0022 東京都立川市柴崎町2-3-6 第一生命ビル1F
TEL:[志學舎]042-519-3325 [東進]042-522-1616
![]() [公式]志學舎Youtubeチャンネルもよろしく!
[公式]志學舎Youtubeチャンネルもよろしく!
![]() [公式]志學舎東進Youtubeチャンネルもよろしく!
[公式]志學舎東進Youtubeチャンネルもよろしく!

志學舎ではSNSで情報発信中!ブックマーク登録、チャンネル登録をお願いします!

人気ブログランキング
↑受験カテゴリー1位!応援クリックよろしく!






